Later this week, a dozen or more Oscar people are converging in Kaiserslautern to discuss the next steps in the part of Oscar that is making use of the programming language Julia. Specifically, we will be discussing some of the technical issues in integrating Polymake, Singular and GAP with the Antic "cornerstone", which is written entirely in Julia and C.
One of the agenda items is a demonstration of a new Julia package which Oleksandr Motsak and I have written, called Singular.jl [2]. It's part of a two pronged strategy with regard to the integration of Singular into Oscar.
The first part of that strategy will be to write an interpreter for the Singular programming language in Julia, so as to take advantage of JIT compilation in Singular. The second part of the strategy is Singular.jl, which I'll describe in detail here.
Singular.jl consists of two parts. The first is a low level interface to Singular [3]. It makes use of Julia's ability to interface to C++ (even templated code) in real time [4]. Julia has the ability to mix C++ code with Julia code and have it all compile down to LLVM instructions for execution by the JIT. It makes use of the Clang library to compile arbitrary C++ code.
This low-level interface to Singular preserves Singular type and function names, and does not make use of garbage collection at the Julia level. Calling a Singular kernel function in this way should have no significant overhead as compared with calling it in a C++ program. You can see this interface layer in the libsingular directory of Singular.jl.
On top of this low-level interface is a garbage collected high level interface, which is compatible with the Nemo generics system. In this way, we make Singular functionality, including the Groebner basis engine, directly accessible to Nemo [5] and the other parts of the Julia/Antic ecosystem.
Nemo provides various generic mathematical structures and algorithms, e.g. dense linear algebra, univariate polynomials (and more recently multivariate), residue rings, fraction fields, power series and so on. By implementing the interface required by Nemo, other packages can make use of all this generic functionality over ring implementations provided by those packages (hardly a novel concept for computer algebra systems, but an important one nonetheless).
Eventually we will also allow Singular to build polynomial rings over rings and fields provided by Nemo and other systems. Singular has this capacity, due to work of Hannes Schoenemann and others, and Oleksandr Motsak already prototyped making Nemo rings available as coefficient rings to Singular as part of the due diligence we did for the big grant we applied for.
So far in Singular.jl we have high level Julia wrappers for Singular integers, rationals, prime fields, integer residue rings, finite fields, polynomials, ideals, modules, vectors, matrices and resolutions.
It's time to see Singular.jl in action. Here is how it looks when Singular.jl is started up. It has a dependency on Nemo, so you see the Nemo.jl welcome message.
We start with creating the Singular integer ring with a Nemo residue ring over it. This is specialised by Singular.jl to actually make use of a Singular residue ring behind the scenes.
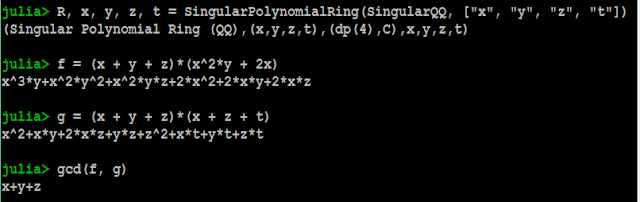
Now let's create a Singular polynomial ring, some polynomials and do a computation with them. Because I didn't specify an ordering, it defaults to the Singular dp ordering (degrevlex) and the ordering, C, for module generators.
One can specify an optional parameter (ordering) to change the polynomial ordering. (Later on, we may separate the module ordering so that it is not needed unless creating module elements. At present, a suitable default is selected automatically.)
Next, we create some ideals over this polynomial ring, count the number of generators and manipulate the generators, using Julia array syntax (which can be overloaded for any purpose).
Next, let's create a Singular ideal and take its standard basis (Groebner basis), using the Singular std command. Singular can compute Groebner bases over all the basic coefficient rings that it supports internally. (The functionality is there to compute them over externally supplied coefficient fields, though it is considered less well tested at this point.)
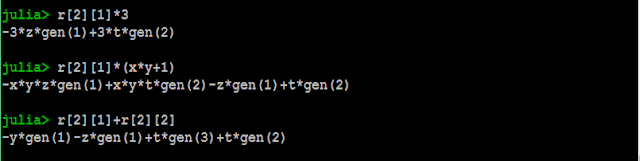
The next most logical thing to do is to compute the syzygy matrix of an ideal. This displays by default as a linear combination of module generators, but it is also possible to convert to a matrix representation.
One of the things we need to improve in the near future is the formatting for the matrix printing. For now, we just did the easiest thing in Singular.jl.
Of course, one can do basic ideal arithmetic.
The next thing one might wish to do is compute resolutions. At present, only the Schreyer resolution is available in Singular.jl. We'll add La Scala and minimal resolutions soon.
One can of course access all the modules in the resolution, precisely as one would expect.
And of course, doing arithmetic on module elements works just as expected.
And naturally, one can compute standard bases and resolutions of modules.
Finally, let's have a demonstration of a computation using the new generic multivariate polynomial code in Nemo (only available in the mpoly development branch at present), over a Singular coefficient ring. Here Singular is not computing the GCD, but Nemo is. And of course it is faster than the native functionality in Singular itself.
That's all for now. In coming blogs I'll talk more about the Singular interpreter and make updates about Oscar development as information comes to hand.
[1] https://wbhart.blogspot.de/2016/11/new-computer-algebra-system-oscar_20.html
[2] https://github.com/wbhart/Singular.jl
[3] https://www.singular.uni-kl.de/
[4] https://github.com/Keno/Cxx.jl
[5] https://github.com/wbhart/Nemo.jl










where is Magma in this discussion? I had used it in my undergraduate days and it was awesome.
ReplyDelete